Рекурсия – жемчужина теории алгоритмов

ВИКТОР КОХОВЕЦ
учитель информатики и математики Валищенской средней школы Пинского района


В информатике в понятие «рекурсия» вкладывается следующий смысл: это прием программирования, при котором подпрограмма вызывает саму себя либо непосредственно, либо косвенно.

Звучит просто, но, как только мы начинаем знакомиться с ней или знакомить наших наиболее способных учеников, появляется много вопросов и проблем: что, зачем и как это вообще работает?

Так зачем же нужна рекурсия? Нельзя ли обойтись без нее? Есть ли у нее преимущества в сравнении с более простыми и доступными для понимания приемами?

В теории алгоритмов есть теорема, которая говорит о том, что рекурсия и итерация эквивалентны. Это значит, что любой алгоритм, который можно реализовать рекурсивно, с таким же успехом может быть реализован и итеративно, и наоборот. Может, действительно, не стоит тратить на нее время и силы, а использовать только циклы?

Здесь необходимо понимать то, что теория и практика не всегда совпадают. То, что любую рекурсию можно заменить итерацией, совсем не значит, что этот итерационный код будет компактным, понятным и быстро работающим. Существует огромное количество задач, для которых именно рекурсивное решение является оптимальным. Например, алгоритмы быстрой сортировки, работы с деревьями, построения фракталов, обхода графов и многие другие. Именно в них рекурсия показывает свою мощь, опережая любые другие реализации по скорости работы и компактности кода.

Но применение рекурсии не всегда оправданно. Есть очень много примеров, в которых применение рекурсии просто расточительно и не выдерживает никакой конкуренции с итерацией. К таким примерам можно отнести и задачи, на которых обычно и объясняют работу рекурсивных алгоритмов: нахождение факториала числа и вычисление чисел ряда Фибоначчи.

Обычно задачи, в которых использование рекурсии имеет смысл, являются далеко не тривиальными. В них часто необходимо использовать такой прием, как разбиение задачи на простые шаги, каждый из которых тоже можно разложить на более мелкие шаги и так далее, пока не доберемся до самых элементарных «шажочков». Такие задачи не по силам большинству учащихся, и знакомство с рекурсией, как мне кажется, является целесообразным только на занятиях с высокомотивированными детьми, при подготовке к олимпиадам и конкурсам по информатике.

Но на самом деле рекурсия – это тонкий и изящный инструмент, который при умелом использовании способен сослужить добрую службу. Задача программиста – не только овладеть обоими подходами, но и научиться выбирать, какой из них применить в том или ином конкретном случае.

Scratch дает замечательную возможность легко изучить основные алгоритмические структуры: следование, ветвление, циклы и подпрограммы. Легкость обусловлена наглядностью кода и отсутствием языковых проблем.

Уже начиная с версии 2.0 в Scratch появилась возможность использовать рекурсивный вызов блока «Другие блоки». Давайте посмотрим, как с его помощью можно легко разобраться в принципах организации и работы рекурсивных алгоритмов.

Иногда для того, чтобы понять, как необходимо действовать правильно, стоит рассмотреть противоположный случай и сделать неправильно. Сейчас мы поступим именно так. Рассмотрим элементарный алгоритм, в котором реализован рекурсивный вызов: «Пример неправильного рекурсивного алгоритма» .

Несомненно, что этот алгоритм является рекурсивным, так как в подпрограмме «Следующий шаг» есть вызов ее же самой. Запустив скрипт, мы увидим, что кот бесконечно «ходит» по сторонам квадрата и, когда он делает следующий шаг, переменная «Глубина рекурсии» увеличивается на единицу.

Самое интересное начнется, если мы включим Турборежим (Редактировать / Включить Турборежим) и откроем вкладку Процессы в Диспетчере задач Windows (Ctrl+Alt+Del / Диспетчер задач / Подробнее). Там мы сможем увидеть, что с каждой секундой объем памяти, занимаемый браузером, возрастает. Если не прервать выполнение программы, то ресурсы системы будут исчерпаны и работа завершится аварийно. У меня на глубине рекурсии около 10 миллионов вкладка с проектом стала занимать больше 2 Гб оперативной памяти, а затем прекратила работу:

Этот пример показывает, что каждый вызов рекурсии занимает дополнительную память на хранение стека вызовов, хотя и расходует ее довольно экономно. Безусловно, в таком виде использовать рекурсию нельзя!

Правильный рекурсивный алгоритм должен содержать в себе условие, которое проверяется перед рекурсивным вызовом. В рекурсивной подпрограмме всегда должны быть два случая: рекурсивный и граничный. Рекурсивный случай – когда подпрограмма вызывает саму себя, а граничный – когда подпрограмма перестает себя вызывать. Наличие граничного случая и предотвращает бесконечную работу алгоритма.

Давайте рассмотрим, как это работает, на примере алгоритма рисования фрактального дерева.

Мы будем двигаться от простого к сложному и начнем с рисования простейшей части дерева – ветки. Создадим новую подпрограмму с помощью блока «Другие блоки». Назовем ее «Дерево1» и будем передавать в нее длину рисуемой ветки. Никакой рекурсии – опускаем перо и делаем 50 шагов вперед и столько же назад.

Следующий уровень – блок «Дерево2». В любом дереве есть развилки, поэтому и мы нарисуем развилку. Рисуем прямую линию и отходящие от нее два дерева первого уровня (с помощью предыдущей подпрограммы) меньшего размера, а затем возвращаемся в первоначальную точку. Никакой магии, никакой рекурсии.

Движемся дальше – блок «Дерево3». На третьем уровне снова рисуем прямую линию и отходящие от нее два дерева, но уже не первого, а второго уровня, опять же используя уже созданные подпрограммы. Снова никакой рекурсии, все обычно и просто, но мы уже начинаем видеть дерево.

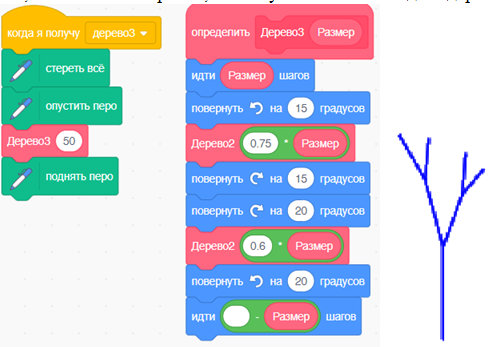
Понятно, что этот процесс можно продолжить и создать подпрограммы «Дерево4», «Дерево5», «Дерево6» и так далее, получая с каждым шагом все более интересные рисунки.

Но зачем делать много новых скриптов? Легко можно заметить, что «Дерево2» и «Дерево3» отличаются друг от друга только цифрами в названиях процедур. Давайте добавим в определение блока еще один параметр – «Уровень» – и при вызове блока «Дерево» будем уменьшать его на единицу. Также необходимо заметить, что блок «Дерево1» не вызывал никаких других блоков, поэтому этот случай в новом блоке рассмотрен отдельно.

Это уже рекурсивный алгоритм. Причем он организован правильно и содержит в себе и граничный случай (когда переменная Уровень равна 1), и рекурсивный (ветка «Иначе»).

Немного доработаем его – добавим возможность изменять числа, которые используются в нем, а также добавим случайный фактор, который будет влиять на эти числа. Результат доступен по адресу . На большой глубине рекурсии необходимо выполнять в Турборежиме.

Как видно из этого примера, довольно простой рекурсивный алгоритм позволяет строить сложные фрактальные деревья. Итерационная реализация будет гораздо сложнее.

Рассмотрим еще один интересный рекурсивный алгоритм. Его можно встретить во многих книгах по программированию, но в Scratch его еще не рассматривали. Речь идет о задаче о ханойских башнях.

В одной из древних легенд говорится следующее. «В храме Бенареса находится бронзовая плита с тремя алмазными стержнями. На один из стержней Бог при сотворении мира нанизал 64 диска разного диаметра из чистого золота так, что наибольший диск лежит на бронзовой плите, а остальные образуют пирамиду, сужающуюся кверху. Это башня Брамы. Работая день и ночь, жрецы переносят диски с одного стержня на другой, следуя законам Брамы:

1. Диски можно перемещать с одного стержня на другой только по одному;

2. Нельзя класть больший диск на меньший.

Когда все 64 диска будут перенесены с одного стержня на другой, и башня, и храмы, и жрецы-брамины превратятся в прах, и наступит конец света».

Эта древняя легенда породила задачу о ханойских башнях: переместить m дисков с одного из трех стержней на другой, соблюдая «законы Брамы».

Пронумеруем стержни слева направо от 1 до 3. Задача состоит в переносе m дисков с левого стержня на правый.

Задача может быть решена одним перемещением только для одного (m = 1) диска. В общем случае потребуется минимум  перемещение.

Построим математическое рекурсивное решение задачи, состоящее из трех этапов:

1. Перенести башню, состоящую из m – 1 диска, со стержня № 1 на стержень № 2;

2. Перенести один оставшийся диск со стержня № 1 на стержень № 3;

3. Перенести башню, состоящую из m – 1 диска, со стержня № 2 на стержень № 3.

Таким образом, задача о перемещении m дисков сводится к задаче о перемещении m – 1 диска. Обращаясь опять к этому же алгоритму, сведем задачу к перемещению m – 2 дисков. Продолжая этот процесс, получим в конце концов задачу о перемещении одного диска. Эта задача решается за один ход. Таким образом, в процессе решения возникают промежуточные задачи: переместить башню из нескольких n дисков с одного стержня на другой.

Обозначим тот стержень, с которого следует снять диски, через i1, а тот, на который надеть, через i2. Тогда номер вспомогательного стержня равен 6 – i1 – i2.

Оформим алгоритм решения задачи о переносе башни из n дисков с i1 на i2 в виде нового блока с тремя параметрами: n, i1, i2:

Решение задачи о ханойских башнях доступно на сайте Scratch по ссылке https://scratch.mit.edu/projects/190497395/.

Помимо текстового решения там размещены анимированные реализации, которые представляют собой игры-головоломки. Они позволяют попробовать решить задачу самому, а затем сравнить свое решение с решением компьютера: https://scratch.mit.edu/projects/217088119/ и https://scratch.mit.edu/projects/190485662/.

Все использованные в статье проекты собраны встудию «Рекурсия в Scratch»: https://scratch.mit.edu/studios/4413241/. В ней есть еще несколько интересных рекурсивных алгоритмов.